| 12.2.62 logand, logandc1, logandc2, logeqv, logior, lognand, lognor, lognot, logorc1, logorc2, logxor | Function |
- Syntax:
-
logand
&rest integers
 result-integer
result-integer
logandc1 integer-1 integer-2
 result-integer
result-integer
logandc2 integer-1 integer-2
 result-integer
result-integer
logeqv &rest integers
 result-integer
result-integer
logior &rest integers
 result-integer
result-integer
lognand integer-1 integer-2
 result-integer
result-integer
lognor integer-1 integer-2
 result-integer
result-integer
lognot integer
 result-integer
result-integer
logorc1 integer-1 integer-2
 result-integer
result-integer
logorc2 integer-1 integer-2
 result-integer
result-integer
logxor &rest integers
 result-integer
result-integer
- Arguments and Values:
-
integers - integers.
integer - an integer.
integer-1 - an integer.
integer-2 - an integer.
result-integer - an integer.
- Description:
-
The functions
logandc1,
logandc2,
logand,
logeqv,
logior,
lognand,
lognor,
lognot,
logorc1,
logorc2,
and logxor
perform bit-wise logical operations on their arguments,
that are treated as if they were binary.
The next figure lists the meaning of each of the functions. Where an `identity' is shown, it indicates the value yielded by the function when no arguments are supplied.
Bit-wise Logical Operations on Integers Function Identity Operation performed logandc1 - and complement of integer-1 with integer-2 logandc2 - and integer-1 with complement of integer-2 logand -1 and logeqv -1 equivalence (exclusive nor) logior 0 inclusive or lognand - complement of integer-1 and integer-2 lognor - complement of integer-1 or integer-2 lognot - complement logorc1 - or complement of integer-1 with integer-2 logorc2 - or integer-1 with complement of integer-2 logxor 0 exclusive or Negative integers are treated as if they were in two's-complement notation.
- Examples:
-
(logior 1 2 4 8)
 15
(logxor 1 3 7 15)
15
(logxor 1 3 7 15)  10
(logeqv)
10
(logeqv)  -1
(logand 16 31)
-1
(logand 16 31)  16
(lognot 0)
16
(lognot 0)  -1
(lognot 1)
-1
(lognot 1)  -2
(lognot -1)
-2
(lognot -1)  0
(lognot (1+ (lognot 1000)))
0
(lognot (1+ (lognot 1000)))  999
;;; In the following example, m is a mask. For each bit in
;;; the mask that is a 1, the corresponding bits in x and y are
;;; exchanged. For each bit in the mask that is a 0, the
;;; corresponding bits of x and y are left unchanged.
(flet ((show (m x y)
(format t "~%m = #o~6,'0O~%x = #o~6,'0O~%y = #o~6,'0O~%"
m x y)))
(let ((m #o007750)
(x #o452576)
(y #o317407))
(show m x y)
(let ((z (logand (logxor x y) m)))
(setq x (logxor z x))
(setq y (logxor z y))
(show m x y))))
999
;;; In the following example, m is a mask. For each bit in
;;; the mask that is a 1, the corresponding bits in x and y are
;;; exchanged. For each bit in the mask that is a 0, the
;;; corresponding bits of x and y are left unchanged.
(flet ((show (m x y)
(format t "~%m = #o~6,'0O~%x = #o~6,'0O~%y = #o~6,'0O~%"
m x y)))
(let ((m #o007750)
(x #o452576)
(y #o317407))
(show m x y)
(let ((z (logand (logxor x y) m)))
(setq x (logxor z x))
(setq y (logxor z y))
(show m x y))))
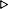 m = #o007750
m = #o007750
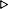 x = #o452576
x = #o452576
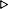 y = #o317407
y = #o317407
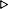
 m = #o007750
m = #o007750
 x = #o457426
x = #o457426
 y = #o312557
y = #o312557
 NIL
NIL
- Exceptional Situations:
-
Should signal type-error if any argument is not an integer.
- See Also:
-
boole
- Notes:
-
(logbitp k -1) returns true for all values of k.
Because the following functions are not associative, they take exactly two arguments rather than any number of arguments.
(lognand n1 n2) ==(lognot (logand n1 n2)) (lognor n1 n2) ==(lognot (logior n1 n2)) (logandc1 n1 n2) ==(logand (lognot n1) n2) (logandc2 n1 n2) ==(logand n1 (lognot n2)) (logiorc1 n1 n2) ==(logior (lognot n1) n2) (logiorc2 n1 n2) ==(logior n1 (lognot n2)) (logbitp j (lognot x)) ==(not (logbitp j x))
- Allegro CL Implementation Details:
- None.