| 12.2.21 asin, acos, atan | Function |
- Syntax:
-
asin
number
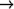 radians
radians
acos number
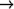 radians
radians
atan number1 &optional number2
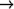 radians
radians
- Arguments and Values:
-
number - a number.
number1 - a number if number2 is not supplied, or a real if number2 is supplied.
number2 - a real.
radians - a number (of radians).
- Description:
-
asin, acos, and atan
compute the arc sine, arc cosine, and arc tangent respectively.
The arc sine, arc cosine, and arc tangent (with only number1 supplied) functions can be defined mathematically for number or number1 specified as x as in the next figure.
Mathematical definition of arc sine, arc cosine, and arc tangent Function Definition Arc sine -i log (ix+ sqrt(1-x2 ))Arc cosine ( pi /2) - arcsin xArc tangent -i log ((1+ix) sqrt(1/(1+x2)))These formulae are mathematically correct, assuming completely accurate computation. They are not necessarily the simplest ones for real-valued computations.
If both number1 and number2 are supplied for atan, the result is the arc tangent of
number1/number2 . The value of atan is always between - pi (exclusive) and pi (inclusive) when minus zero is not supported. The range of the two-argument arc tangent when minus zero is supported includes - pi .For a real number1, the result is a real and lies between - pi /2 and pi /2 (both exclusive). number1 can be a complex if number2 is not supplied. If both are supplied, number2 can be zero provided number1 is not zero.
The following definition for arc sine determines the range and branch cuts:
arcsin z = -ilog ( iz+sqrt(1-z2))The branch cut for the arc sine function is in two pieces: one along the negative real axis to the left of -1 (inclusive), continuous with quadrant II, and one along the positive real axis to the right of 1 (inclusive), continuous with quadrant IV. The range is that strip of the complex plane containing numbers whose real part is between - pi /2 and pi /2. A number with real part equal to - pi /2 is in the range if and only if its imaginary part is non-negative; a number with real part equal to pi /2 is in the range if and only if its imaginary part is non-positive.
The following definition for arc cosine determines the range and branch cuts:
arccos z = pi /2-arcsin zor, which are equivalent,
arccos z = -ilog (z+i sqrt(1-z2))arccos z = 2log (sqrt((1+z)/2) + i (sqrt(1-z)/2))/iThe branch cut for the arc cosine function is in two pieces: one along the negative real axis to the left of -1 (inclusive), continuous with quadrant II, and one along the positive real axis to the right of 1 (inclusive), continuous with quadrant IV. This is the same branch cut as for arc sine. The range is that strip of the complex plane containing numbers whose real part is between 0 and pi . A number with real part equal to 0 is in the range if and only if its imaginary part is non-negative; a number with real part equal to pi is in the range if and only if its imaginary part is non-positive.
The following definition for (one-argument) arc tangent determines the range and branch cuts:
arctan z =log (1+iz) -log (1-iz) /2iBeware of simplifying this formula; "obvious" simplifications are likely to alter the branch cuts or the values on the branch cuts incorrectly. The branch cut for the arc tangent function is in two pieces: one along the positive imaginary axis above i (exclusive), continuous with quadrant II, and one along the negative imaginary axis below -i (exclusive), continuous with quadrant IV. The points i and -i are excluded from the domain. The range is that strip of the complex plane containing numbers whose real part is between - pi /2 and pi /2. A number with real part equal to - pi /2 is in the range if and only if its imaginary part is strictly positive; a number with real part equal to pi /2 is in the range if and only if its imaginary part is strictly negative. Thus the range of arc tangent is identical to that of arc sine with the points - pi /2 and pi /2 excluded.
For atan, the signs of number1 (indicated as x) and number2 (indicated as y) are used to derive quadrant information. The next figure details various special cases. The asterisk (*) indicates that the entry in the figure applies to implementations that support minus zero.
Quadrant information for arc tangent y Condition x Condition Cartesian locus Range of result y = 0 x > 0 Positive x-axis 0 * y = +0 x > 0 Positive x-axis +0 * y = -0 x > 0 Positive x-axis -0 y > 0 x > 0 Quadrant I 0 < result < pi /2 y > 0 x = 0 Positive y-axis pi /2 y > 0 x < 0 Quadrant II pi /2 < result < pi y = 0 x < 0 Negative x-axis pi * y = +0 x < 0 Negative x-axis + pi * y = -0 x < 0 Negative x-axis - pi y < 0 x < 0 Quadrant III - pi < result < - pi /2 y < 0 x = 0 Negative y-axis - pi /2 y < 0 x > 0 Quadrant IV - pi /2 < result < 0 y = 0 x = 0 Origin undefined consequences * y = +0 x = +0 Origin +0 * y = -0 x = +0 Origin -0 * y = +0 x = -0 Origin + pi * y = -0 x = -0 Origin - pi - Examples:
-
(asin 0)
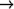 0.0
(acos #c(0 1))
0.0
(acos #c(0 1)) 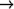 #C(1.5707963267948966 -0.8813735870195432)
(/ (atan 1 (sqrt 3)) 6)
#C(1.5707963267948966 -0.8813735870195432)
(/ (atan 1 (sqrt 3)) 6) 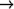 0.087266
(atan #c(0 2))
0.087266
(atan #c(0 2)) 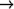 #C(-1.5707964 0.54930615)
#C(-1.5707964 0.54930615)
- Exceptional Situations:
-
acos and asin should signal an error of type type-error if number is not a number.
atan should signal type-error if
one argument is supplied and that argument is not a number,
or if two arguments are supplied and both of those arguments are not reals.
acos, asin, and atan might signal arithmetic-error.
- See Also:
-
log,
sqrt,
Section 12.1.3.3 Rule of Float Substitutability
- Notes:
-
The result of either asin or acos can be a complex
even if number is not a complex; this occurs when the
absolute value of number is greater than one.
- Allegro CL Implementation Details:
- None.