| 12.2.60 boole | Function |
- Syntax:
-
boole
op integer-1 integer-2
 result-integer
result-integer
- Arguments and Values:
-
Op - a bit-wise logical operation specifier.
integer-1 - an integer.
integer-2 - an integer.
result-integer - an integer.
- Description:
-
boole performs bit-wise logical operations on
integer-1 and integer-2, which are treated as if
they were binary and in two's complement representation.
The operation to be performed and the return value are determined by op.
boole returns the values specified for any op in the next figure.
Bit-Wise Logical Operations Op Result boole-1 integer-1 boole-2 integer-2 boole-andc1 and complement of integer-1 with integer-2 boole-andc2 and integer-1 with complement of integer-2 boole-and and boole-c1 complement of integer-1 boole-c2 complement of integer-2 boole-clr always 0 (all zero bits) boole-eqv equivalence (exclusive nor) boole-ior inclusive or boole-nand not-and boole-nor not-or boole-orc1 or complement of integer-1 with integer-2 boole-orc2 or integer-1 with complement of integer-2 boole-set always -1 (all one bits) boole-xor exclusive or - Examples:
-
(boole boole-ior 1 16)
 17
(boole boole-and -2 5)
17
(boole boole-and -2 5)  4
(boole boole-eqv 17 15)
4
(boole boole-eqv 17 15)  -31
;;; These examples illustrate the result of applying BOOLE and each
;;; of the possible values of OP to each possible combination of bits.
(progn
(format t "~&Results of (BOOLE <op> #b0011 #b0101) ...~
~% - Op---- - Decimal-- - Binary- - Bits - ~%")
(dolist (symbol '(boole-1 boole-2 boole-and boole-andc1
boole-andc2 boole-c1 boole-c2 boole-clr
boole-eqv boole-ior boole-nand boole-nor
boole-orc1 boole-orc2 boole-set boole-xor))
(let ((result (boole (symbol-value symbol) #b0011 #b0101)))
(format t "~& ~A~13T~3,' D~23T~:*~5,' B~31T ...~4,'0B~%"
symbol result (logand result #b1111)))))
-31
;;; These examples illustrate the result of applying BOOLE and each
;;; of the possible values of OP to each possible combination of bits.
(progn
(format t "~&Results of (BOOLE <op> #b0011 #b0101) ...~
~% - Op---- - Decimal-- - Binary- - Bits - ~%")
(dolist (symbol '(boole-1 boole-2 boole-and boole-andc1
boole-andc2 boole-c1 boole-c2 boole-clr
boole-eqv boole-ior boole-nand boole-nor
boole-orc1 boole-orc2 boole-set boole-xor))
(let ((result (boole (symbol-value symbol) #b0011 #b0101)))
(format t "~& ~A~13T~3,' D~23T~:*~5,' B~31T ...~4,'0B~%"
symbol result (logand result #b1111)))))
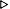 Results of (BOOLE <op> #b0011 #b0101) ...
Results of (BOOLE <op> #b0011 #b0101) ...
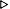 - Op---- - Decimal-- - Binary- - Bits -
- Op---- - Decimal-- - Binary- - Bits -
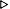 BOOLE-1 3 11 ...0011
BOOLE-1 3 11 ...0011
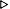 BOOLE-2 5 101 ...0101
BOOLE-2 5 101 ...0101
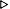 BOOLE-AND 1 1 ...0001
BOOLE-AND 1 1 ...0001
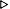 BOOLE-ANDC1 4 100 ...0100
BOOLE-ANDC1 4 100 ...0100
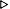 BOOLE-ANDC2 2 10 ...0010
BOOLE-ANDC2 2 10 ...0010
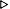 BOOLE-C1 -4 -100 ...1100
BOOLE-C1 -4 -100 ...1100
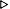 BOOLE-C2 -6 -110 ...1010
BOOLE-C2 -6 -110 ...1010
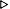 BOOLE-CLR 0 0 ...0000
BOOLE-CLR 0 0 ...0000
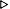 BOOLE-EQV -7 -111 ...1001
BOOLE-EQV -7 -111 ...1001
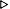 BOOLE-IOR 7 111 ...0111
BOOLE-IOR 7 111 ...0111
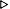 BOOLE-NAND -2 -10 ...1110
BOOLE-NAND -2 -10 ...1110
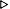 BOOLE-NOR -8 -1000 ...1000
BOOLE-NOR -8 -1000 ...1000
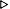 BOOLE-ORC1 -3 -11 ...1101
BOOLE-ORC1 -3 -11 ...1101
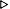 BOOLE-ORC2 -5 -101 ...1011
BOOLE-ORC2 -5 -101 ...1011
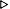 BOOLE-SET -1 -1 ...1111
BOOLE-SET -1 -1 ...1111
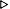 BOOLE-XOR 6 110 ...0110
BOOLE-XOR 6 110 ...0110
 NIL
NIL
- Exceptional Situations:
-
Should signal type-error if its first argument is not a
bit-wise logical operation specifier or if any subsequent argument is not
an integer.
- See Also:
-
logand
- Notes:
-
In general,
(boole boole-and x y) ==(logand x y)
Programmers who would prefer to use numeric indices rather than bit-wise logical operation specifiers can get an equivalent effect by a technique such as the following:
;; The order of the values in this `table' are such that ;; (logand (boole (elt boole-n-vector n) #b0101 #b0011) #b1111) => n (defconstant boole-n-vector (vector boole-clr boole-and boole-andc1 boole-2 boole-andc2 boole-1 boole-xor boole-ior boole-nor boole-eqv boole-c1 boole-orc1 boole-c2 boole-orc2 boole-nand boole-set)) BOOLE-N-VECTOR
(proclaim '(inline boole-n))
BOOLE-N-VECTOR
(proclaim '(inline boole-n))
 implementation-dependent
(defun boole-n (n integer &rest more-integers)
(apply #'boole (elt boole-n-vector n) integer more-integers))
implementation-dependent
(defun boole-n (n integer &rest more-integers)
(apply #'boole (elt boole-n-vector n) integer more-integers))
 BOOLE-N
(boole-n #b0111 5 3)
BOOLE-N
(boole-n #b0111 5 3)  7
(boole-n #b0001 5 3)
7
(boole-n #b0001 5 3)  1
(boole-n #b1101 5 3)
1
(boole-n #b1101 5 3)  -3
(loop for n from #b0000 to #b1111 collect (boole-n n 5 3))
-3
(loop for n from #b0000 to #b1111 collect (boole-n n 5 3))
 (0 1 2 3 4 5 6 7 -8 -7 -6 -5 -4 -3 -2 -1)
(0 1 2 3 4 5 6 7 -8 -7 -6 -5 -4 -3 -2 -1)
- Allegro CL Implementation Details:
- None.