| 12.2.23 sinh, cosh, tanh, asinh, acosh, atanh | Function |
- Syntax:
-
sinh
number
 result
result
cosh number
 result
result
tanh number
 result
result
asinh number
 result
result
acosh number
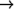 result
result
atanh number
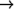 result
result
- Arguments and Values:
-
number - a number.
result - a number.
- Description:
-
These functions compute the hyperbolic sine, cosine, tangent,
arc sine, arc cosine, and arc tangent functions,
which are mathematically defined for an argument x
as given in the next figure.
Mathematical definitions for hyperbolic functions Function Definition Hyperbolic sine (ex-e-x)/2 Hyperbolic cosine (ex+e-x)/2 Hyperbolic tangent (ex-e-x)/(ex+e-x) Hyperbolic arc sine log (x+sqrt(1+x2))Hyperbolic arc cosine 2 log (sqrt((x+1)/2) + sqrt((x-1)/2))Hyperbolic arc tangent ( log (1+x) -log (1-x))/2The following definition for the inverse hyperbolic cosine determines the range and branch cuts:
arccosh z = 2log (sqrt((z+1) /2) + sqrt((z-1)/2)).The branch cut for the inverse hyperbolic cosine function lies along the real axis to the left of 1 (inclusive), extending indefinitely along the negative real axis, continuous with quadrant II and (between 0 and 1) with quadrant I. The range is that half-strip of the complex plane containing numbers whose real part is non-negative and whose imaginary part is between - pi (exclusive) and pi (inclusive). A number with real part zero is in the range if its imaginary part is between zero (inclusive) and pi (inclusive).
The following definition for the inverse hyperbolic sine determines the range and branch cuts:
arcsinh z =log (z+sqrt(1+z2)).The branch cut for the inverse hyperbolic sine function is in two pieces: one along the positive imaginary axis above i (inclusive), continuous with quadrant I, and one along the negative imaginary axis below -i (inclusive), continuous with quadrant III. The range is that strip of the complex plane containing numbers whose imaginary part is between - pi /2 and pi /2. A number with imaginary part equal to - pi /2 is in the range if and only if its real part is non-positive; a number with imaginary part equal to pi /2 is in the range if and only if its imaginary part is non-negative.
The following definition for the inverse hyperbolic tangent determines the range and branch cuts:
arctanh z = (log (1+z) -log (1-z))/2.Note that:
i
arctan z =arctanh iz.The branch cut for the inverse hyperbolic tangent function is in two pieces: one along the negative real axis to the left of -1 (inclusive), continuous with quadrant III, and one along the positive real axis to the right of 1 (inclusive), continuous with quadrant I. The points -1 and 1 are excluded from the domain. The range is that strip of the complex plane containing numbers whose imaginary part is between - pi /2 and pi /2. A number with imaginary part equal to - pi /2 is in the range if and only if its real part is strictly negative; a number with imaginary part equal to pi /2 is in the range if and only if its imaginary part is strictly positive. Thus the range of the inverse hyperbolic tangent function is identical to that of the inverse hyperbolic sine function with the points - pi i/2 and pi i/2 excluded.
- Examples:
-
(sinh 0)
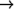 0.0
(cosh (complex 0 -1))
0.0
(cosh (complex 0 -1)) 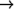 #C(0.540302 -0.0)
#C(0.540302 -0.0)
- Exceptional Situations:
-
Should signal an error of type type-error if number is not a number.
Might signal arithmetic-error.
- See Also:
-
log,
sqrt,
Section 12.1.3.3 Rule of Float Substitutability
- Notes:
-
The result of acosh may be a complex even if number
is not a complex; this occurs when number is less than one.
Also, the result of atanh may be a complex even if number
is not a complex; this occurs when the absolute value of number
is greater than one.
The branch cut formulae are mathematically correct, assuming completely accurate computation. Implementors should consult a good text on numerical analysis. The formulae given above are not necessarily the simplest ones for real-valued computations; they are chosen to define the branch cuts in desirable ways for the complex case.
- Allegro CL Implementation Details:
- None.