| 12.2.19 floor, ffloor, ceiling, fceiling, truncate, ftruncate, round, fround | Function |
- Syntax:
-
floor number &optional divisor  quotient,
remainder
quotient,
remainderffloor number &optional divisor  quotient,
remainder
quotient,
remainderceiling number &optional divisor  quotient,
remainder
quotient,
remainderfceiling number &optional divisor  quotient,
remainder
quotient,
remaindertruncate number &optional divisor  quotient,
remainder
quotient,
remainderftruncate number &optional divisor  quotient,
remainder
quotient,
remainderround number &optional divisor  quotient,
remainder
quotient,
remainderfround number &optional divisor  quotient,
remainder
quotient,
remainder - Arguments and Values:
-
number - a real.
divisor - a non-zero real. The default is the integer 1.
quotient - for floor, ceiling, truncate, and round: an integer; for ffloor, fceiling, ftruncate, and fround: a float.
remainder - a real.
- Description:
-
These functions divide number by divisor,
returning a quotient and remainder, such that
quotient·divisor+remainder=number
The quotient always represents a mathematical integer. When more than one mathematical integer might be possible (i.e., when the remainder is not zero), the kind of rounding or truncation depends on the operator:
- floor, ffloor
floor and ffloor produce a quotient that has been truncated toward negative infinity; that is, the quotient represents the largest mathematical integer that is not larger than the mathematical quotient.
- ceiling, fceiling
ceiling and fceiling produce a quotient that has been truncated toward positive infinity; that is, the quotient represents the smallest mathematical integer that is not smaller than the mathematical result.
- truncate, ftruncate
truncate and ftruncate produce a quotient that has been truncated towards zero; that is, the quotient represents the mathematical integer of the same sign as the mathematical quotient, and that has the greatest integral magnitude not greater than that of the mathematical quotient.
- round, fround
round and fround produce a quotient that has been rounded to the nearest mathematical integer; if the mathematical quotient is exactly halfway between two integers, (that is, it has the form integer+1/2), then the quotient has been rounded to the even (divisible by two) integer.
All of these functions perform type conversion operations on numbers.
The remainder is an integer if both x and y are integers, is a rational if both x and y are rationals, and is a float if either x or y is a float.
ffloor, fceiling, ftruncate, and fround handle arguments of different types in the following way: If number is a float, and divisor is not a float of longer format, then the first result is a float of the same type as number. Otherwise, the first result is of the type determined by contagion rules; see Section 12.1.1.2 Contagion in Numeric Operations.
- floor, ffloor
- Examples:
-
(floor 3/2)
 1, 1/2
(ceiling 3 2)
1, 1/2
(ceiling 3 2)  2, -1
(ffloor 3 2)
2, -1
(ffloor 3 2)  1.0, 1
(ffloor -4.7)
1.0, 1
(ffloor -4.7)  -5.0, 0.3
(ffloor 3.5d0)
-5.0, 0.3
(ffloor 3.5d0)  3.0d0, 0.5d0
(fceiling 3/2)
3.0d0, 0.5d0
(fceiling 3/2)  2.0, -1/2
(truncate 1)
2.0, -1/2
(truncate 1)  1, 0
(truncate .5)
1, 0
(truncate .5)  0, 0.5
(round .5)
0, 0.5
(round .5)  0, 0.5
(ftruncate -7 2)
0, 0.5
(ftruncate -7 2)  -3.0, -1
(fround -7 2)
-3.0, -1
(fround -7 2)  -4.0, 1
(dolist (n '(2.6 2.5 2.4 0.7 0.3 -0.3 -0.7 -2.4 -2.5 -2.6))
(format t "~&~4,1@F ~2,' D ~2,' D ~2,' D ~2,' D"
n (floor n) (ceiling n) (truncate n) (round n)))
-4.0, 1
(dolist (n '(2.6 2.5 2.4 0.7 0.3 -0.3 -0.7 -2.4 -2.5 -2.6))
(format t "~&~4,1@F ~2,' D ~2,' D ~2,' D ~2,' D"
n (floor n) (ceiling n) (truncate n) (round n)))
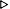 +2.6 2 3 2 3
+2.6 2 3 2 3
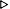 +2.5 2 3 2 2
+2.5 2 3 2 2
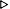 +2.4 2 3 2 2
+2.4 2 3 2 2
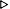 +0.7 0 1 0 1
+0.7 0 1 0 1
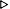 +0.3 0 1 0 0
+0.3 0 1 0 0
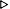 -0.3 -1 0 0 0
-0.3 -1 0 0 0
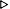 -0.7 -1 0 0 -1
-0.7 -1 0 0 -1
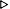 -2.4 -3 -2 -2 -2
-2.4 -3 -2 -2 -2
 -2.5 -3 -2 -2 -2
-2.5 -3 -2 -2 -2
 -2.6 -3 -2 -2 -3
-2.6 -3 -2 -2 -3
 NIL
NIL
- Notes:
-
When only number is given, the two results are exact;
the mathematical sum of the two results is always equal to the
mathematical value of number.
(function number divisor) and (function (/ number divisor)) (where function is any of one of floor, ceiling, ffloor, fceiling, truncate, round, ftruncate, and fround) return the same first value, but they return different remainders as the second value. For example:
(floor 5 2)
 2, 1
(floor (/ 5 2))
2, 1
(floor (/ 5 2))  2, 1/2
2, 1/2
If an effect is desired that is similar to round, but that always rounds up or down (rather than toward the nearest even integer) if the mathematical quotient is exactly halfway between two integers, the programmer should consider a construction such as (floor (+ x 1/2)) or (ceiling (- x 1/2)).
- Allegro CL Implementation Details:
- None.